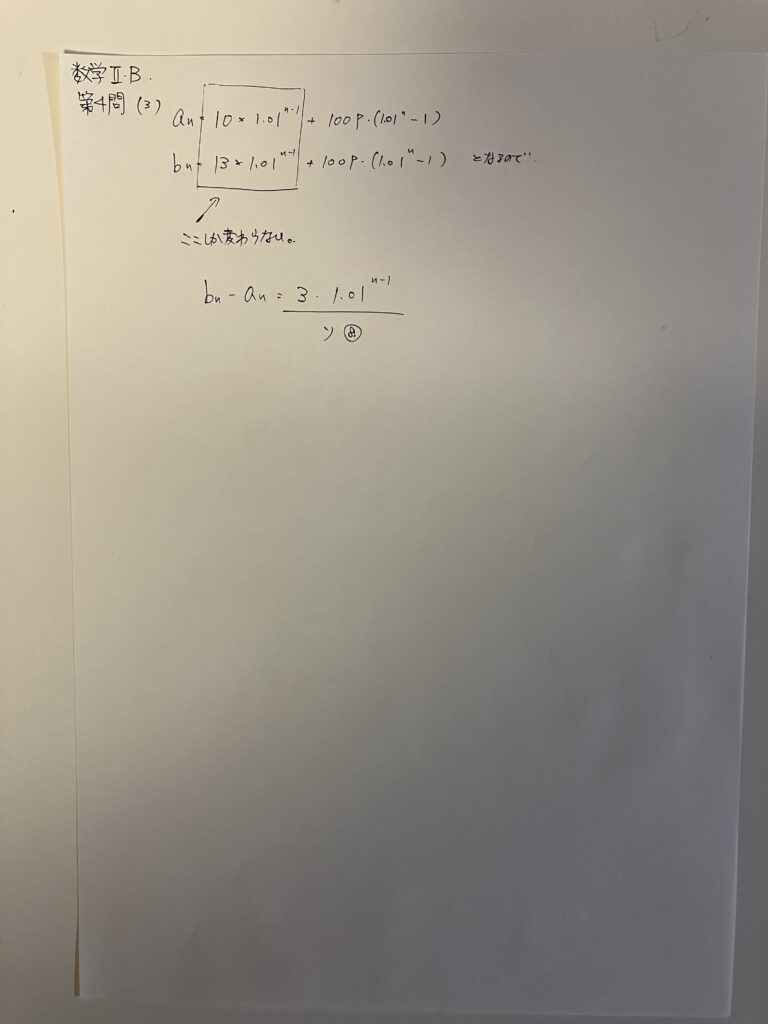いつも精神論よりですが算数数学塾なのでたまに数学の専門的な事も書きたいと思います。ただこれは約47万人(その内数学は35万人)の大勢の受験生が毎年受けている話で、全然遠い話ではないんですね。僕が受けたのは丁度20年前ですが、より思考力や、実生活と数学の繋がりを考える想像力が問われている気がします。そして今後はデータ分析や確率統計も必修に入るそうです。これは完全に時代の流れで、我が国でどの様な人材を育てたいかも密接に反映されています。僕も習ってない範囲が少しずつ出てくるので勉強しないといけないですね。
この先、思考力、想像力、データ。このあたりは確実にキーワードになると思います。(というか既になっています。)人口増加フェーズで品質の良い商品を低コストで製造する時代で日本は一時代を築きましたが、これからは全くの新しいサービスを創造できるか、そこが日本を浮上させるカギになる。まさに思考力、発想力が必要だ。またこれからIoT(Internet of Things)で全てのモノのデータが取れ、それを分析するデータサイエンスが必要だ。そんな話を良く目にします。僕はわりかしそうなると思っています。算数・数学は本当に大切です。
さて、今年の共通テストの数学を解きましたが昨年より易化していました。
平均点も集計途中との事ですが、数ⅠA/37.96→58.08点、数ⅡB/43.06→64.86点と両方とも昨年より平均点が20点ほど上がっています。共通テストの難易度は毎年読めないですね。
僕は、共通テストは非常に良い問題だと思っています。特に本質への理解度、基本的な事をどれだけしっかりと理解できているか、思考力が問われており、小さい頃からしっかり基本と思考力を積み上げる事が大切だと感じます。またより一層、実生活に関する問題が増えていて、実生活と数学を関連付ける想像力も必要です。
例えば、数学ⅡB 第2問 積分と桜の開花時期の関係性は、素晴らしい問題でした。(添付5枚目)
どういう問題かというと、ソメイヨシノが開花するタイミングについてAくんとBさんが話し合っていて、この二人が、横軸が時間、縦軸が気温として、グラフを書いて、その面積がある400を超えたら開花するという仮説を立てるんですね。
つまり一日の温度を計測して、暖かい日もあれば寒い日もあって気温は上下しながら推移しますが、合計400を超えたら開花するという仮説です。
僕は面白い仮説だなと思いました。(ネットで調べたら400℃の法則とかあるので、正しいのかもしれないですね。)
ここでの大きなポイントは、三つです。
- 積分を面積としてとらえられているか。
- ソメイヨシノの開花=温度の合計で決まる、という文中の仮説をイメージできたか。
- ①と②を関連付けられたか。
共通テストの面白いところは、深く理解できている人はすらすら解けて、理解が浅い人にとっては地獄の様な計算を強いられる(=時間が足りない&得点取れない)仕組みがちりばめられています。
今回は、二人の会話で、「今回は温度がずっと上がり続けているよね。だから30~40日と、40~50日はこんな関係になるよね。」という会話があります。
専門用語であれば単調増加の為、幅が一定の場合は面積も増加する。よって40~50日の方が大きいとなります。
実はこれ、あえて平易な言葉を使いますと「グラフがずっと右肩上がりで、幅10日間を切り抜いたら、右の方が左より面積でかいやん。」これだけの話なんですね。
計算しなくても少し考えれば小学生でも気付ける様な話になっています。考えずにペンを走らせるのではなく、少し立ち止って考える癖を持つことが大事です。
40~50日の面積をゴリゴリ計算した学生は時間が足りなくなったと思います。共通テストは本質に対する理解の深さで点数がばらつく様に作りこまれているんですよね。
これには続きがあって面白いです。0~30日が面積180、30~40日が面積115であることが与えられています。そして上より40~50日は面積115より大きいとなります。
この時、開花したタイミングが分かるね!と二人の会話で出てきて、開花のタイミングを問われます。
答えは40日~50日の間に咲きます。
40日までの面積は180+115=295
50日までの面積は295+(115より大きい数字)=410より大きい数字。
じゃあ、400を超えるのは40~50日の間のどこかになります。
おもろい。共通テスト作った人凄すぎる・・・
積分に対する理解の深さ、想像力(ソメイヨシノの開花と合計温度の関係)、積分とソメイヨシノの開花の関連付け。
いわゆる思考力が必要で、単純に数式を覚えたり計算だけでは絶対に解けない問題なんですよね。
積分が面積であるという基本をどれだけ理解できているか。普段からすぐに計算したり、答えを見たりせずに思考する癖。
難しい問題に時間をかけて取り組むのも共通テストに活きると思います。
共通テストで高得点取るのって、実は四則演算が早いことも大事ですが、それ以上にどれだけ思考する回数を積み上げてきたかの方が大事なんですよね。
第4問の毎年一定金額の貯蓄をして、年利1%で考えたら、何年後にいくらになっているか。これを等比数列の漸化式と繋げる素晴らしい問題です。(添付6枚目、7枚目)
漸化式の作り方や、等比数列の基本を捉えていれば、簡単に解けます。
積分も数列もベクトルも共通テストの問題は、全て基本をしっかり抑えたらちゃんと解けます。そしてスピードを高める為には思考力が必要になります。実生活を数式に繋げる想像力も必要です。
基礎、思考力、想像力、このあたりが必要です。
僕自身も現役の時はあり得ないほど難しい問題に3時間ほど挑戦してそれでも解けなくて答えを見るという勉強もしてました。一見非効率で無駄なのかもしれませんが、意味はあります。脳みそに負荷をかける事は大事です。脳みそでダンベル上げる感じです。
脳みそに汗をかかしている分、センター試験は余裕になりますし、京大の2次試験でも、もっと難しい問題を沢山解いているので簡単に見えます。勉強に近道はなく日頃から一生懸命に鍛錬を積み上げるのみですね。
現在高校2年生の塾生が在籍しておりますので、この一年間に基本を捉えた良問且つ難問を沢山解いてもらって、塾生を志望校に導ける様に一緒に頑張っていきたいと思います。